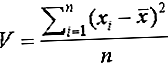definícia takejto vety
V 5. storočí pred naším letopočtom došlo na území Grécka k intelektuálnemu hnutiu, ktoré možno považovať za počiatok racionálneho myslenia a vedeckej mentality. Jedným z mysliteľov, ktorý viedol nový intelektuálny kurz, bol Thales z Milétu, ktorý je považovaný za prvý predsokratovský prúd, myšlienkový prúd, ktorý prelomil mýtické myslenie a urobil prvé kroky vo filozofickej a vedeckej činnosti.
Pôvodné Thalesove diela sa nezachovali, ale prostredníctvom ďalších mysliteľov a historikov sú známe jeho hlavné príspevky: predpovedal zatmenie Slnka roku 585 pred Kr. C obhajoval myšlienku, že voda je pôvodným prírodným prvkom, a vynikal aj ako matematik. Jeho najuznávanejším prínosom je veta, ktorá nesie jeho meno. Podľa legendy inšpirácia pre vetu pochádza z Thalesovej návštevy Egypta a obrazu pyramíd.
Talesova veta
Základná myšlienka vety je jednoduchá: dve rovnobežné čiary preťaté priamkou, ktorá vytvára dva uhly. Jedná sa o dva uhly, ktoré sú zhodné, to znamená, že oba uhly majú rovnakú mieru (sú tiež známe ako zodpovedajúce uhly, jeden je na vonkajšej strane rovnobežiek a druhý na vnútornej strane).
Je potrebné mať na pamäti, že niekedy existujú dve Thalesove vety (jedna odkazuje na podobné trojuholníky a druhá na príslušné uhly, ale obe vety sú založené na rovnakom matematickom princípe).
Špecifické aplikácie
Geometrický prístup k Thalesovej vete má zrejmé praktické dôsledky. Pozrime sa na konkrétny príklad: 15 m vysoká budova vrhá 32 metrový tieň a v rovnakom okamihu vrhá jednotlivec 2,10 metrový tieň. S týmito údajmi je možné poznať výšku uvedeného jedinca, pretože je potrebné vziať do úvahy, že uhly, ktoré vrhajú ich tiene, sú zhodné. Takže s údajmi v úlohe a princípom Thalesovej vety o zodpovedajúcich uhloch je možné poznať výšku jednotlivca jednoduchým pravidlom troch (výsledok by bol 0,98 m).
Vyššie uvedený príklad jasne ilustruje, že Thalesova veta má veľmi rozmanité aplikácie: pri štúdiu geometrických mierok a metrických vzťahov geometrických útvarov. Tieto dve otázky čistej matematiky sa premietajú do ďalších teoretických a praktických oblastí: pri vypracovávaní plánov a máp, v architektúre, poľnohospodárstve alebo strojárstve.
Na záver by sme si mohli pripomenúť kuriózny paradox: že hoci Thales z Milétu žil pred 2 600 rokmi, jeho veta sa naďalej študuje, pretože ide o základný princíp geometrie.
Foto: iStock - Rawpixel Ltd.
