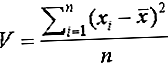definícia parametra
Parametre sú definované ako tie premenné a konštanty, ktoré sa vyskytujú v matematickom výraze, pričom jeho variáciou sa vytvárajú rôzne riešenia problému. Týmto spôsobom parameter predpokladá numerické znázornenie enormného množstva informácií, ktoré sú odvodené zo štúdie premennej. Jeho výpočet sa zvyčajne vykonáva pomocou aritmetického vzorca, ktorý bol predtým vypracovaný z údajov získaných od populácie.
V oblasti počítačového programovania sa použitie pojmu parameter často používa na označenie vnútornej vlastnosti procedúry.
Prečo sú parametre dôležité?
Keď matematik uvažuje o štúdiu premennej, musí čeliť množstvu údajov, ktoré sú prezentované neusporiadane. Preto je nevyhnutná predchádzajúca práca s týmito informáciami, ktorá je obmedzená a objednaná, aby fungovala jednoduchšie a efektívnejšie.
Aj keď koncentrácia počiatočných údajov v parametri znamená stratu časti informácií v nich obsiahnutých, je to značne kompenzované tým, že je možné vykonať porovnanie medzi vzorkami alebo umožniť charakterizáciu údajov.
Hlavné štatistické parametre
V rámci štatistík možno rozlíšiť tri veľké skupiny parametrov: polohu, rozptyl a tvar.
Merania polohy umožňujú identifikovať hodnotu, okolo ktorej sú údaje väčšinou zoskupené. Existujú dva typy parametrov disperzie: tie s centrálnou tendenciou (stredná hodnota, mód a medián) a tie s necentrálnou pozíciou (percentily, decily a kvartily).
Disperzné opatrenia zase slúžia na zhrnutie distribúcie údajov. Problém týchto parametrov spočíva v tom, že samy osebe nie sú dostatočné na zjednodušenie informácií, takže je nevyhnutné, aby boli sprevádzané ďalšími doplňujúcimi parametrami, ktoré poskytujú informácie o heterogenite údajov.
Medzi najvýznamnejšie parametre disperzie patria rozptyl, štandardná odchýlka, variačné koeficienty a rozsah.
Napokon tvarové parametre označujú tvar histogramu údajov, najbežnejším znázornením je gaussovský zvon. Tu stojí za to zdôrazniť koeficienty šikmosti a špičatosti.
Okrem toho existujú ďalšie štatistické parametre, ktoré sa používajú na konkrétny účel, napríklad index Gini na meranie nerovnosti.
Fotografie: iStock - mediaphotos / Jovanmandic
